前回の続きになります。前回は具体的な量子ゲートについて扱いました。今回は量子ゲートを用いて、加算器とシフト表を作ってみましょう。

基本アルゴリズムへの第一歩
現代のコンピュータが「0」か「1」かの世界で計算を行うのに対し、量子コンピュータは「0でもあり1でもある」という量子の世界の不思議な性質を利用して、桁違いの計算能力を実現しようとしています。この新しい計算機は、私たちの社会が抱える複雑な問題を解決する鍵となる可能性を秘めています。
しかし、「量子コンピュータ」と一言で言っても、その実現方法にはいくつかの種類があり、それぞれに得意なこと、不得意なことがあります。まずは、その代表的な2つの方式、「ゲート型」と「アニーリング型」の違いを解き明かし、特に汎用性が高いとされるゲート型コンピュータが得意とするアルゴリズムについて、簡単にご紹介します。
量子コンピュータの種類「ゲート型」「アニーリング型」
量子コンピュータは、現在主に「ゲート型」と「アニーリング型」という2つのアプローチで開発が進められています。これらは似て非なるもので、目的や仕組みが大きく異なります。
まず「アニーリング型」は、特定の種類の問題、すなわち「組み合わせ最適化問題」を解くことに特化した専用計算機と言えます。これは、多数の選択肢の中から最も良い組み合わせを見つけ出す問題に特化しており、例えば、無数の経路から最適な配送ルートを導き出したり、全従業員の希望を考慮しながら最も効率的なシフトを組んだり、金融市場でリスクとリターンのバランスが取れた最適な資産の組み合わせを見つけたりといった用途で力を発揮します。ただし、その能力は最適化問題に限定されるため、私たちが普段使うコンピュータのように、多様な計算をこなす汎用性はありません。
https://annealing-cloud.com/ja/knowledge/2.html
(アニーリングマシンの詳細な説明が載っています。是非ご覧ください)
アニーリングマシンについて重要な
一方の「ゲート型」は、私たちが現在使っているコンピュータ(古典コンピュータ)のように、汎用的な計算を行うことを目指した万能選手です。この方式では、「量子ゲート」と呼ばれる基本操作を組み合わせて「量子回路」を作り、さまざまなアルゴリズムを実行します。原理上はあらゆる計算が可能で、古典コンピュータでは現実的な時間で解くことが困難な問題を高速に解く能力を秘めています。しかし、その万能性と引き換えに大きな課題も抱えています。量子の状態は非常にデリケートで、外部の僅かなノイズでも計算エラーが発生しやすいため、高度な誤り訂正技術が不可欠です。また、エラーを抑えながら計算の規模を大きくすることが難しく、実用化に向けてはまだ多くの技術的ハードルが残されています。
最近は研究が進んでおり、組み合わせ最適化のみのアニーリング型よりも、汎用的で応用できる範囲が多く、世界を変える可能性がゲート型の方が大きいからか盛んに研究が行われており、近年では日本でも以下のような状況が続いております。
「ゲート型」が得意なこと
ゲート型量子コンピュータの真価は、その汎用性と、古典コンピュータを圧倒する特定の「量子アルゴリズム」を実行できる点にあります。
その代表格が、非常に大きな数字を素数の積に分解する「ショアのアルゴリズム」です。現在のインターネットを支える暗号技術の多くは、この素因数分解が従来のコンピュータでは極めて困難であるという事実を安全性の根拠にしています。ゲート型コンピュータがこの計算を現実的な時間で解いてしまう能力を持つことは、未来のセキュリティに大きな変革をもたらすことを意味します。
また、「グローバーのアルゴリズム(あとで紹介します)」は、整理されていない膨大なデータの中から特定のものを探し出す検索作業を劇的に高速化します。古典コンピュータではデータ量に比例して検索時間が増えていきますが、このアルゴリズムを使えば、その平方根に比例する時間で済むため、データが巨大になればなるほど、その差は歴然となります。
さらに、ゲート型コンピュータは、新薬の開発や新しい素材の発見につながる量子シミュレーションの領域で、計り知れない可能性を秘めています。物質や分子の性質は量子の世界の法則に支配されており、その複雑な振る舞いを古典コンピュータで正確に再現することは事実上不可能です。ゲート型コンピュータは、量子のルールを直接利用してシミュレーションを行うため、これまで到達できなかったレベルでの高精度な計算が実現します。
具体的な実装
論理回路と量子コンピュータ
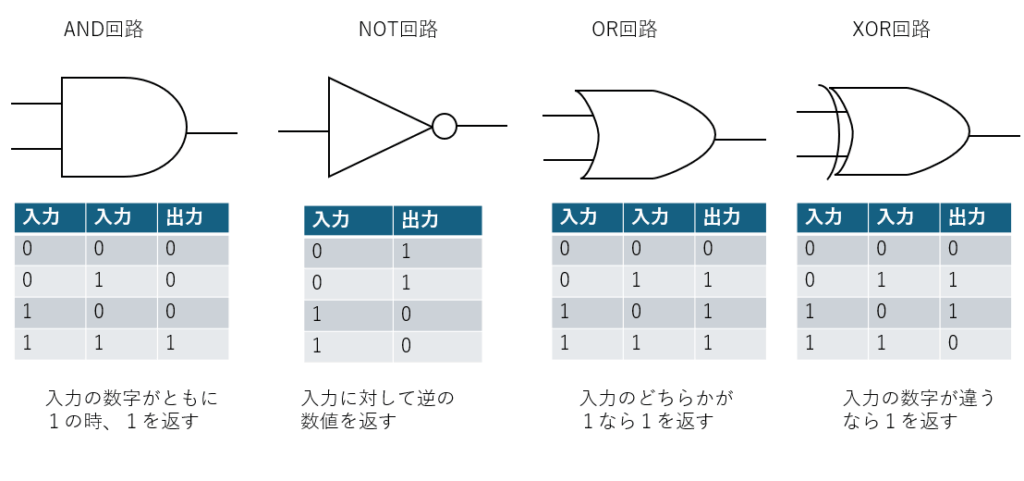
論理回路とは?
論理回路とは、コンピュータが「計算」や「判断」を行うための最も基本的な電子回路です。これは、情報を「0」と「1」の2つの状態(ビット)で表現し、いくつかの入力ビットを受け取って、決められたルールに基づき1つの出力ビットを返す仕組みです。(古典コンピュータ上の足し算や引き算のようなものから、複雑な演算まで、この論理回路の組み合わせで表現されています。)
基本的な論理回路であるNOT回路、AND回路、OR回路についてはまず説明をします。
量子コンピュータでの実装
今回は量子回路上で比較的実装が容易なNOT回路とXOR回路について説明します。(ANDとORについて気になる人は調べてみてね!)
NOT回路
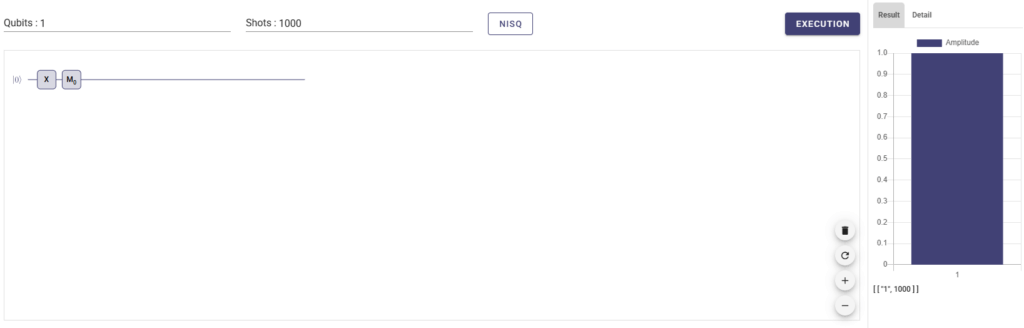
量子コンピュータ上でNOT回路っぽい挙動(明らかにスピンをπ倒すことと、出力結果を反転させることは異なる概念なので、NOT回路っぽいと言っておきます)を実現するためにはXゲートを通せばよさそうです。
XOR回路
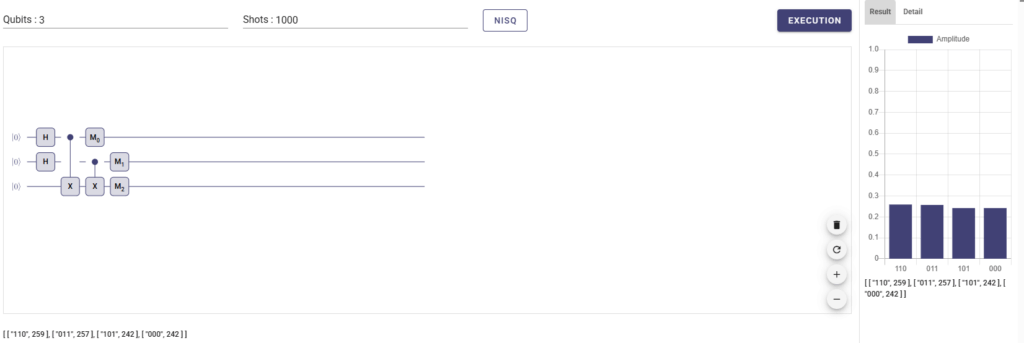
まず、ここでCXゲートを使ってみましょう。CXゲートは制御ビットが|1>のときターゲットビットを反転させる効果を持ちましたね。この場合はこのようにして、量子回路を組んであげます。そうすると、それぞれが1量子ビット目と2量子ビット目が|0>|0>の時はそのまま何も反応せず0を返して、|1>|1>の時は二回反転が行われて0を返してちょうどXOR回路のようになります。
足し算を実装してみよう!
まず、加算器を作る前に「足し算の仕組み」について考察していきましょう。今回は1桁+1桁の場合のみを考えましょう。
2進数における一桁+一桁の場合まず考えられるのは繰り上がりです。例えば
1+1 =10(ここでの数値は二進数なので10は十進数では2のことです。)
繰り上がりを実装するためにはまず、XOR回路が必要そうです。1桁目は入力のどちらかが1の場合は1で、両方とも0か1が入力された場合は0になりそうです。
つぎに計算結果の2桁目を考えてみましょう。
二桁目は「入力ビットが|1>|1>なら1を返してそれ以外なら0を返してくれるのよさそうです。ちょうど古典コンピュータにおけるAND回路になりますね。この実装のためには、CCXゲート(Toffoliゲート)と呼ばれるものを使います。
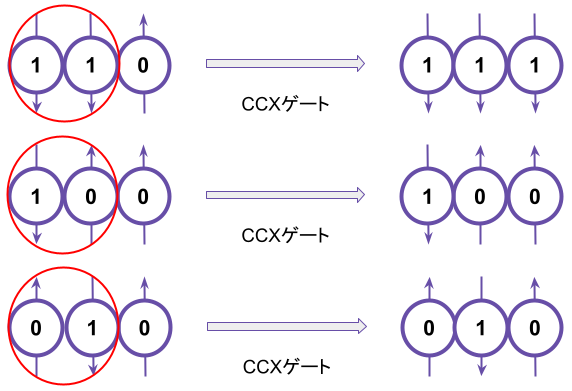
これらのことを加味すると
・1桁目の計算結果はCXゲート二つで実現
・2桁目の計算結果はCCXゲートで実装
となり、次のような量子回路を組むことで加算器は実現できそうですね。
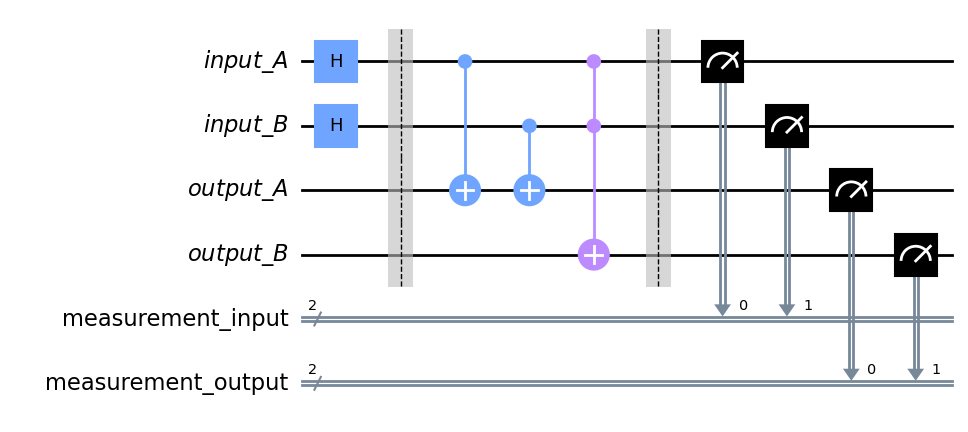
シフト表を作ってみる
実務的な例として、シフト表を作ってみましょう。量子コンピュータは同時にすべての通りを調べることができて、人員配置問題が得意です。
次の例題について考えてみましょう。
**2. シフト希望から勤務表を作成してみよう。**
今までの量子回路は単に計算の方法について説明を行っていきましたが、ここでは現実問題により近い問題を解いてみます。
今回は以下の簡単なシフト希望をもとに勤務表を作成することを考えます。
| 従業員 | 朝 | 昼 | 夜 |
| A | 〇 | × | × |
| B | × | 〇 | 〇 |
| C | 〇 | 〇 |
3人の従業員とシフトには朝・昼・夜の三つがあるとします。
各時間帯で従業員が1名になるような勤務表を作成することを考えます。
この場合答えは明らかですが、A と B さんの2人がシフトに入る場合になります。
では実際に解いてみましょう。
まず、制約について整理していきましょう。
・朝はAさんかCさんのどちらかがシフトに入る
・昼はBさんが入る。
・夜はBさんとCさんのどちらかがシフトに入る。
となります。ここで、条件を満たす場合は1そうでないなら0を返すようにしましょう。まずは朝の条件から作っていきます。
朝の条件
朝はAさんとCさんしかシフト希望を出していないので、この場合はどちらかが入る。つまりXORで実装できるので、2つのCXゲートを足し算の時みたいに使ってやればいいですね。
昼の条件
この場合はBさんしかシフト希望を出していないので、Bさんが1の時に素直に1を返してやればよさそうですね。
夜の条件
BさんかCさんのどちらかがシフトに入ってくれるのがいいので、その場合は朝の条件と同様にCXゲート2つでXOR回路を作ってやれば解けそうです。
この場合、アンシラビットを用意します。アンシラビットとは「計算の際の途中式」や補助的に使うがinputでもoutputでもないビットのことです。「補助量子ビット」と呼ばれます。
順を追って解説していきます。
1.重ね合わせ状態を用意する。
→ABCの全ての通りを一気に計算したいのでまずは量子ビットのアダマールゲートを作用させて重ね合わせ状態を生み出します。

2.制約に合わせて回路を実装していく
→まずさらに「朝」「昼」「夜」のシフトが条件を満たしているかを判断するビットをさらに3つ用意します。この場合、(A,C)のXOR回路と(B,C)のXOR回路、そしてBが1なら「昼」も1にする回路を用意してくればいいです。
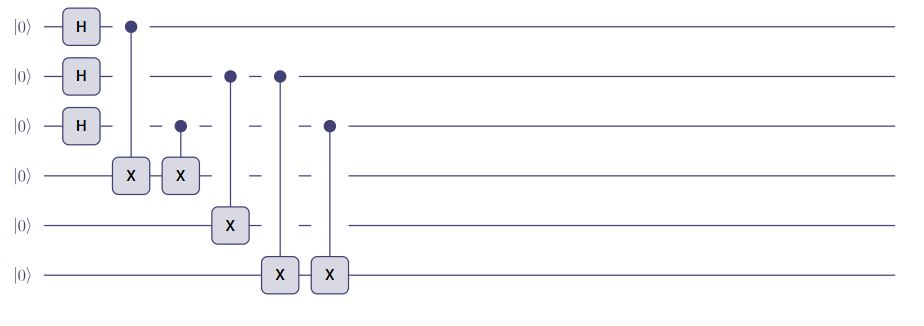
3.組み合わせが条件を満たしていた場合は「1」を返すようにする。
このためには3つの値が1ならば1を一番下の量子ビットが返すようにすればいいです。そのためにはCCXゲートを次のように作用させるとうまくいきます。まず先に作用するCCXゲートで朝と昼それぞれが1ならば1を返すようにします。そして後で作用するCCXゲートで、手前のCCXゲートから1が返ってくることと、夜の場合が1であることを確認すれば、3つの値が1であることを認識できます。この場合、下から2番目の「朝」と「昼」の量子ビットがそれぞれ1であることを、確認するためのビットを「アンシラビット(補助量子ビット)」といいます。
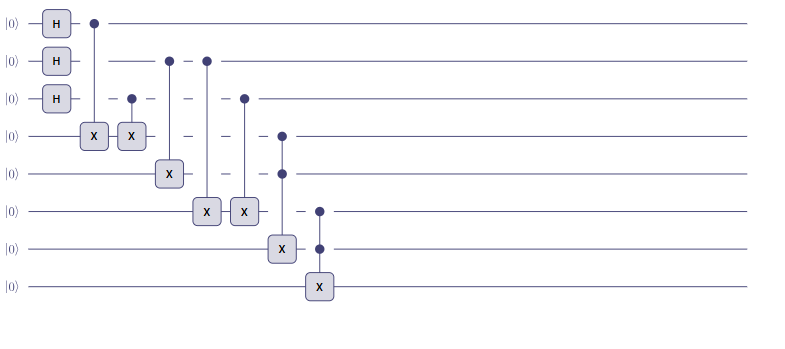
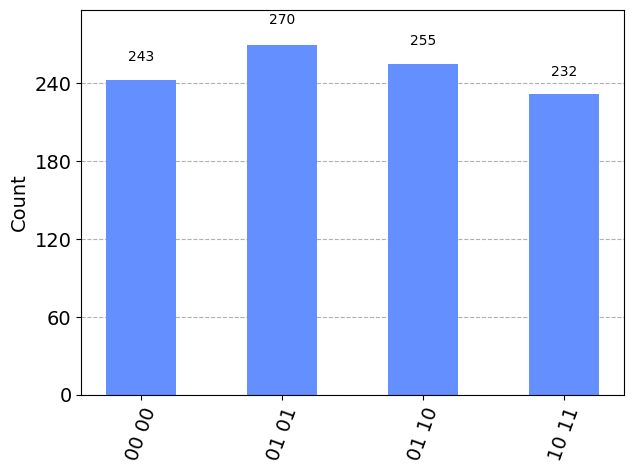
最後にそれぞれの量子ビットを観測します。そして、最後の量子ビットが1になっている組み合わせを探せば終わりです。

この中で一倍最後のビットに1が立っているのは[110111]です。つまり、AさんとBさんがシフトに出れば朝昼夜の全てで出勤人数が一人ずつで条件を満たすということになります。
【コラム】
量子コンピュータにできて古典コンピュータにできない計算は?
「量子コンピュータは古典コンピュータにできない計算ができる」という話をよく耳にしますが、実はこれは少し誤解を招く表現です。計算理論的には、量子コンピュータで解ける問題は、原理的にはすべて古典コンピュータでも解くことができるのです。
チューリングの等価性定理
この根本的な事実は「チューリングの等価性定理」によって説明されます。この定理は、量子コンピュータを含むあらゆる現実的な計算モデルが、古典的なチューリングマシンと本質的に同等の計算能力を持つことを示しています。つまり、量子コンピュータが解ける問題なら、十分な時間と記憶容量があれば古典コンピュータでも必ず解けるということです。
では、なぜ量子コンピュータが「革命的」だと言われるのでしょうか。答えは「効率性」にあります。同じ問題を解くのに必要な時間が、天と地ほど違うのです。
ここ最近の動向
2019年にGoogleが発表した「量子超越性(quantum supremacy)」の実証実験では、古典コンピュータなら1万年かかる特定の問題を、量子コンピュータが200秒で解きました。ただし、これは実用的な問題ではなく、量子コンピュータに有利になるよう設計された人工的な問題でした。
この実験が示したのは、「量子コンピュータが古典コンピュータより圧倒的に速くなりうる問題が実際に存在する」という原理的な可能性です。現在は、この優位性を実用的な問題に応用する段階に入っています。
計算量の概念
コンピュータがどれくらい「頑張らなければならないか」を測る尺度として、計算量という概念があります。これは料理に例えると、10人分の料理を作るのと100人分の料理を作るのでは、必要な時間や材料が違うのと同じように、コンピュータも扱うデータが大きくなればなるほど、より多くの時間や記憶容量が必要になるということです。
アルゴリズムの効率性を示すーBig-O記法
この「頑張り具合」を数学的に表現するのがBig-O記法です。O(1)は「データがどんなに大きくても同じ時間で済む」という理想的な状況で、O(n)は「データが2倍になると時間も2倍かかる」という比例関係を表します。O(n²)になると「データが2倍になると時間は4倍かかる」となり、だんだん厳しくなってきます。
そして最も厄介なのがO(2ⁿ)という指数時間です。これは「データが1つ増えるだけで時間が2倍になる」という恐ろしい増え方をします。例えば、チェスや将棋のように「すべての可能な手を調べる」ような問題では、選択肢が1つ増えるだけで計算時間が倍々ゲームのように膨れ上がってしまうのです。
量子コンピュータの方が効率のいいケース
ここで登場するのが量子コンピュータです。従来のコンピュータでは「これは無理だ」と諦めるしかなかった指数時間の問題の中に、量子コンピュータなら現実的な時間で解けるものがあることが分かってきました。
最も劇的な例が素因数分解問題です。n桁の整数を因数分解する場合、最も効率的な古典アルゴリズムである一般数体篩法でもO(exp((log N)^(1/3) × (log log N)^(2/3)))という準指数時間がかかります。これは実質的に、桁数が増えると指数的に時間が増加することを意味します。2048ビット(約600桁)のRSA鍵を破るには、現在の最高性能のスーパーコンピュータでも何十億年もかかると推定されています。
ところが、Shorのアルゴリズムを使った量子コンピュータなら、同じ問題をO(n³)という多項式時間で解けてしまいます。つまり、桁数が2倍になっても計算時間は8倍にしか増えません。十分な量子ビットを持つ量子コンピュータなら、2048ビットのRSA鍵も数時間から数日で破ることが可能になると予想されています。これが「量子コンピュータが実現すると現在の暗号が破られる」と言われる理由です。
検索問題でも大きな差が現れます。N個の要素からなる未整理のデータベースで特定の項目を探す場合、古典的な線形探索ではO(N)の時間が必要です。つまり平均してN/2回、最悪でN回調べる必要があります。しかし、Groverのアルゴリズムなら同じ問題をO(√N)で解けます。100万件のデータベースなら、古典的手法では最悪100万回必要ですが、量子アルゴリズムなら約1000回で済むのです。この平方根の改善は一見控えめに見えますが、データが大きくなるほどその威力を発揮します。
量子超越は「計算量」だけで実現できない?
コラム:量子超越は「計算量」だけで実現できない?
量子コンピュータが古典コンピュータの能力を遥かに超える「量子超越(または量子優位性)」。この言葉を聞くと、多くの人が理論上の「計算量」の話を思い浮かべるでしょう。古典コンピュータでは指数関数的に時間が増える問題 (O(2n)) を、量子コンピュータなら多項式時間 (O(n2))で解ける、といった話です。
しかし、この理論上の計算量の比較だけで、本当に「超越」は実現できるのでしょうか?答えは「否」です。現実のコンピュータは、理論通りに一瞬で計算を終えるわけではないからです。
Big-O表記の死角
計算量を表すO(ビッグオー)表記は、問題の規模(n)が大きくなったときに、計算ステップが「どのように増えていくか」という伸び率を示すものです。これはアルゴリズムの優劣を比較する上で非常に重要ですが、ある一つの現実的な側面を無視しています。それは「定数倍」の存在、つまり一回の計算ステップに実際にかかる時間です。
例えば、ある古典アルゴリズムが 100×2n ステップかかり、量子アルゴリズムが 1,000,000×n2 ステップかかるとします。nが非常に大きければ量子が圧勝しますが、小さなnでは古典の方が速いかもしれません。この「1,000,000」という定数部分に、量子コンピュータ特有の物理的な制約が隠れているのです。
ゲート時間とショット数という現実
量子コンピュータにおける計算の基本単位は「量子ゲート」です。これは古典コンピュータのNOTやANDゲートに相当しますが、瞬時に動作するわけではありません。超伝導量子ビットをマイクロ波で制御するなど、一つ一つのゲート操作には物理的な時間、ゲート制御時間(数十ナノ秒など)が必要です。アルゴリズムが要求するゲート操作の数が膨大になれば、この時間も無視できません。
さらに決定的なのが「ショット」という概念です。量子計算は確率的な性質を持つため、一度の計算(1ショット)で必ず正しい答えが出るとは限りません。正しい答えを高い確率で得るためには、同じ計算を何千回、何万回と繰り返し実行(ショット)し、統計的に最も頻繁に現れた結果を「答え」として採用する必要があります。
つまり、量子コンピュータがひとつの問題を解くための実際の時間は、おおよそ以下のようになります。
総計算時間≈(1ゲートあたりの時間)×(ゲート操作の数)×(ショット数)
理論上の計算量 (O表記) が語るのは、真ん中の「ゲート操作の数」が問題規模nに対してどう増えるか、という部分だけです。実際の優位性を証明するには、この掛け算全体の結果が、古典スーパーコンピュータの計算時間よりも明確に短くならなければなりません。
量子超越とは、単なる計算量の理論的な勝利宣言ではありません。それは、ゲート制御の速さや精度、そしてショット数をいかに減らせるかといった、物理的・技術的な課題を乗り越えた先にある、現実世界での時間短縮競争のゴールなのです。






































