量子産業元年として迎える2025年
2025年は「国際量子科学技術年(International Year of Quantum Science and Technology:IYQ)」として国連により制定されています。これは、1925年にハイゼンベルクが行列力学と呼ばれる量子力学の定式化を完成させた論文が出版されてから100年という記念すべき節目を迎えるためです。
国連による宣言では、この1年間にわたる世界規模の取り組みは「量子科学とその応用の重要性に対する一般の認識を高めることを目的としたあらゆるレベルの活動を通じて実施される」とされており、量子技術の社会実装に向けた大きな転換点となることが期待されています。
日本においても、大阪大学QIQBが国内初のIYQ公式パートナーに就任するなど、量子技術の発展において重要な役割を担う体制が整いつつあります。2025年は、まさに日本にとっても「量子産業元年」と呼ぶべき年になるでしょう。
ゲート型量子コンピュータとは何か
量子コンピュータは、量子力学の原理を計算に応用した革新的な計算機です。特に「ゲート型量子コンピュータ」は、従来のコンピュータとは根本的に異なる動作原理を持っています。
従来のコンピューターはバイナリ・ビット(0と1)を使用してデータを保管および処理しますが、量子コンピューターは量子ビット(またはキュービット)を重ね合わせて使用することで、さらに多くのデータを一度にエンコードできます。
この「重ね合わせ」という量子力学の現象により、2量子ビットは4ビットの情報を保管でき、3量子ビットは8ビット、4量子ビットは12ビットの情報を保管できます。つまり、量子
ビット数が増えるにつれて、処理可能な情報量が指数関数的に増大するのです。
技術の歴史的発展
量子コンピュータの歴史は1980年代に遡ります。1980年にポール・ベニオフが量子系においてエネルギーを消費せず計算が行えることを示し、1982年にはファインマンも量子計算が古典計算に対し指数関数的に有効ではないかと推測しています。
理論的な発展から実用化への大きな転換点となったのは、1994年にピーター・ショアが実用的なアルゴリズム『ショアのアルゴリズム』を考案し、量子コンピュータの研究に火をつけたことでした。このアルゴリズムにより、従来のコンピュータでは現実的な時間では解けないとされる素因数分解問題が、量子コンピュータでは極めて短時間で解けることが示されました。
近年の企業間競争も激化しています。2016年、グーグルは9量子ビットの量子コンピューターで水素分子をシミュレートしました。2017年、インテルは17量子ビットの量子コンピューターを、IBMは90マイクロ秒にわたって量子状態を維持できる50量子ビットのチップを開発しました。そして2019年、Googleが量子超越性の実証を発表するなど、技術的ブレイクスルーが相次いでいます。
本講座での目的
本講座ではJQCAの「量子エンジニア認定講座(ゲート型エントリー)」の検定問題や解説に基づいて、ゲート型量子コンピュータの基本的な考え方について学ぶ、
なお、本講座では量子ビットを二次元空間上の矢印として扱うが、現実の量子ビットには量子力学特有の「位相」と呼ばれるパラメータがあるため厳密には1量子ビットはブロッホ球上の3次元で表現されることを留意いただきたい。
本講座が量子コンピューティングの考え方や基礎的な演算を学ぶ上で読者の力になれれば幸いです。
なお、本講座の対象者は「中学生以上」となっているが、量子ビットは一般的にベクトルによって表現され、量子ゲートは量子状態に対するユニタリ演算子であることが一般に知られているため、適宜、厳密な理解に基づいた説明を知りたい方は各章ごとにコラムを用意したため、解説本文で物足りなかった人は是非読んでみてください。
1.量子コンピュータと古典コンピュータ
1.1 古典ビットと量子ビット
ビットとは情報の最小単位のことであり、古典コンピュータ上では例えば、「トランジスター上に電気が流れているか流れていないか」のように0と1どちらかの状態を作りその「列」として情報を作り出しています。

古典ビットの取りうる状態の数はビット数nに対して2^n個となります。例えば2古典ビット系を考えれば次のような4つの状態をとることができます。(下の図を参照)

量子ビットとは何か?
1.1 重ね合わせの状態

量子ビットは翻って、あくまでイメージですがボールに矢印が刺さっている描像で書くことができる矢印が上を向いている状態を「0」下を向ている状態を「1」と表現すると、そのほかにも矢印が真横を向いている場合や斜めを向いている状態も量子ビットはとることができる。例えば下図右から3番目の矢印が真横を向いている場合は「0」が50 % 「1」が50%の状態(重ね合わせの状態)と解釈できる。このような状態を「重ね合わせの状態」と呼ぶ。
なお量子ビットの「0」と「1」は古典ビットと分けて考えるために|0>と|1>と表現する。これは「ゼロケット」と呼ぶ。この書き方は量子力学におけるディラックが提案した「ブラケット表記」に由来します。(「コラム1:線形結合」を参照されたし)
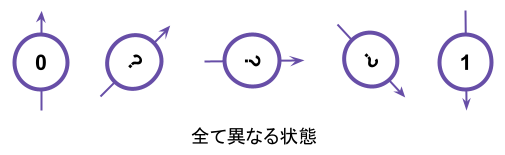
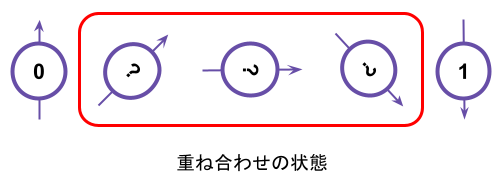
ここで重要なのはこれらがすべて異なる状態であるということです。先ほどは「→が真横を向いている状態は|0>が50 %|1>が50%の状態であると表現しましたが、これはあくまで|0>と|1>とは全く異なる
「|0>が50 %で、|1>が50%の状態0」
という状態です。少しまどろっこしいですね。
この矢印が横向きの状態は一つ例を挙げると
1/√2( |0> + |1> )と書き表せます。言ってしまえば2x+3yという数式には確かにxとyが含まれていますが数式自体はxとyとも全く異なるものを表していますね。このようなイメージです。
1.2 量子もつれ
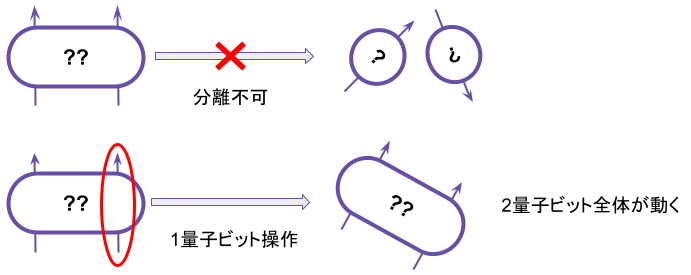
量子もつれ(quantum entanglement)は、2つ以上の量子ビットが強い相関を持ち、個別に記述できない状態になる現象です。
一方の量子ビットを測定すると、もう一方の状態が瞬時に決まります。もつれた量子ビットは強い相関を持つため、例えば2量子ビット系で考えると、1つの量子ビットのみを操作すると2量子ビット全体に影響があります。(2.3 量子もつれとベルの不等式)

1.3 量子ビットの観測
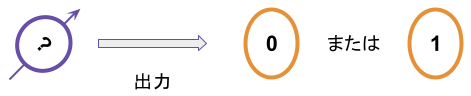
量子ビットを観測するときに実際に得られるのは|0>か|1>の必ずどちらかです。
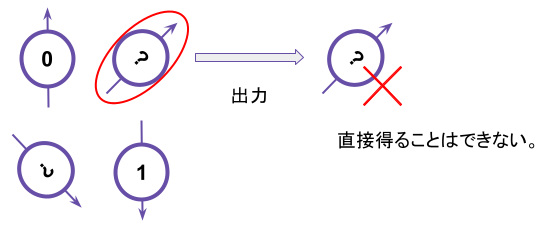
例えば、次のように|0>でも|1>でもない状態を観測すると、それぞれ量子ビットの状態に対応してある一定の確率で「0」または「1」が観測される。例えば先ほど用いた。矢印が真横を向いている量子状態では「0」が50% 「1」が50 %観測される。つまり、1000回観測したら500回「0」が500回は「1」が観測されて。矢印が真横を向いている状態そのものは観測できません。矢印が真上を向いている場合は1000回すべてが「0」が出力されて、真下の場合は1000回すべて「1」が出力されます。

2.量子ゲート
2.1量子ゲートと論理回路
古典コンピュータでは、AND回路やOR回路のような「論理回路」を使って計算を行います。たとえばAND回路は、入力が両方とも1のときにだけ1を出力します。
量子コンピュータでも、これに相当する「量子ゲート(quantum gate)」という操作を用いて計算を行います。量子ゲートとは、量子ビットの状態を変える操作のことです。
この量子ゲートをどのように組み合わせて使うかという設計図のようなものが、「量子アルゴリズム」と呼ばれます。
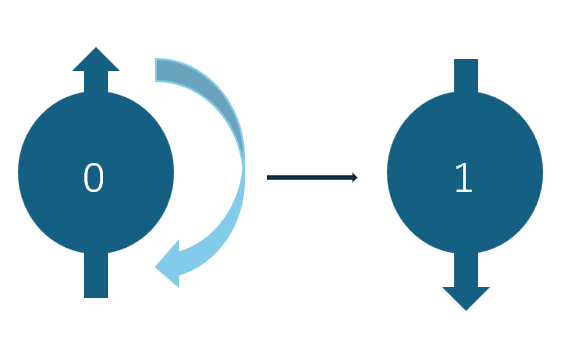
2.1Xゲート
|0⟩ を |1⟩ に、|1⟩ を |0⟩ に変えるゲート。古典のNOTと同じ動作。言ってしまえば、矢印を右周りに180度傾ける操作になる。
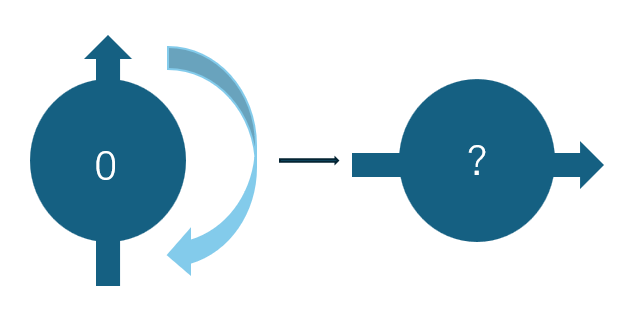
2.2Hゲート
さっきの話でいうところの量子ビットを右回りに90度傾ける操作をしてくれる量子ビット。|0>を90ど傾けると重ね合わせ状態を作ることができるため、このゲートを使って量子特有の性質である重ね合わせ状態を作ってうまく計算を行う。
2.3CXゲート
1つ目の量子ビット(制御ビット)が|1⟩のときだけ、2つ目のビット(ターゲット)にXゲートを適用。この時「ある量子ビットの結果によってもう片方の状態を変える」ということを行っていますね。前者を「制御ビット、後者を「ターゲットビット」と呼びます。
例として実際の量子回路を組んで計算をしてみましょう。
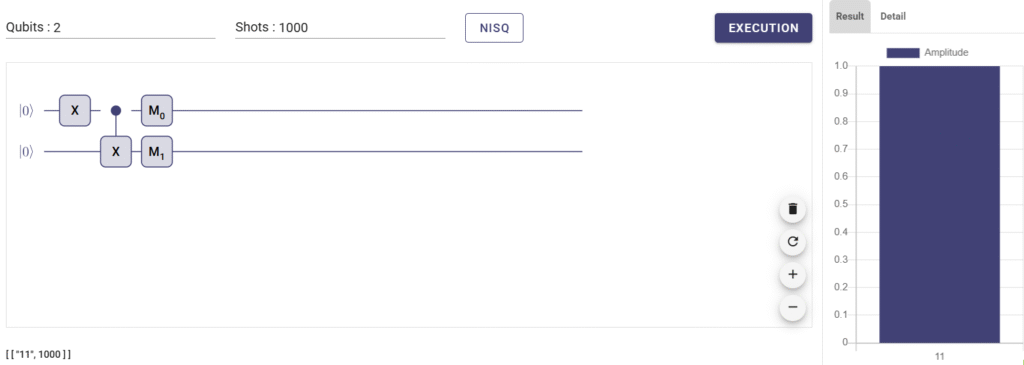
XとM0と書かれている間に挟まれている2量子ビットにかかっているゲートがCXゲートです。ここでは上の量子ビットが制御ビット、下の量子ビットがターゲットビットです。今回は2つの量子ビットとも初期値は|0>ですが、上の量子ビットはXゲートがかかっているのでCXゲートを通る前に、値は|1>になっています。右側が計算結果で、1000回計算して(画面左上のshotsの値が何回計算したかを表している)、1000回とも両方の量子ビットはともに|1>でした。
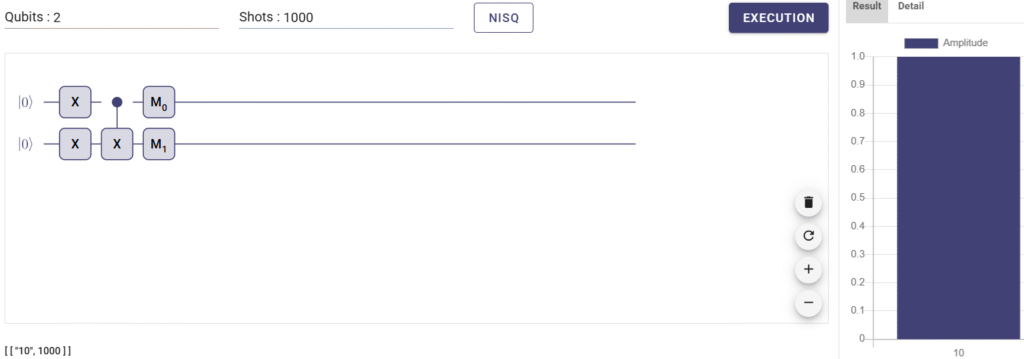
二つとも1だった場合は、ターゲットビットが反転するので、1→0になりました。
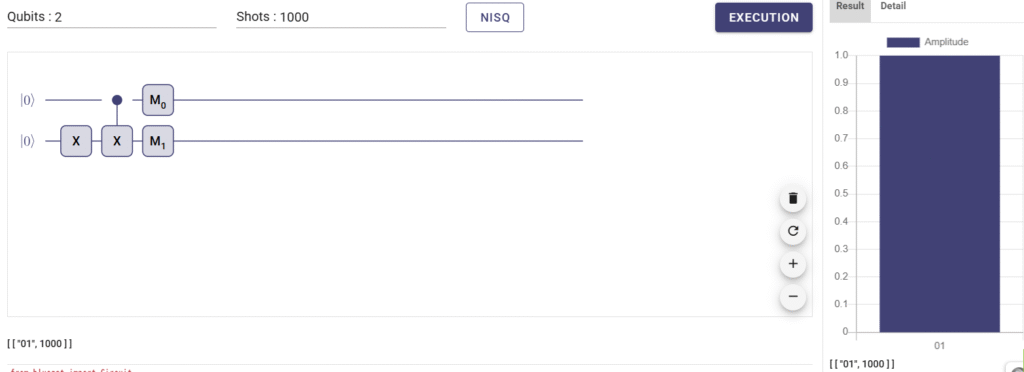
次回は具体的にこれらの量子ゲートを用いて様々な計算を一緒に実装していきましょう。
コラム
・コラム1:ボルンの確率解釈
量子子ビットの状態 (1/√2)(|0⟩ + |1⟩) を見て、「なんで係数が 1/√2 なの?」と疑問に思ったことはありませんか?直感的には、|0⟩と|1⟩が「半々」なら係数は 1/2 でもよさそうなものです。でも実際に測定すると、確かに50%ずつの確率で観測される。この不思議な関係を説明するのが、ボルンの確率解釈です。
ボルンが1926年に提唱したこの解釈によると、量子状態の係数(確率振幅)の絶対値の二乗が、その状態が観測される確率になります。
例えば (1/√2)(|0⟩ + |1⟩) の場合:
- |0⟩が観測される確率:|1/√2|² = 1/2
- |1⟩が観測される確率:|1/√2|² = 1/2
だから係数は 1/√2 なのです!
この「二乗則」は単なる数学的便宜ではありません。量子力学の干渉現象を正しく記述するために必要なのです。
確率振幅は複素数で、位相という情報も持っています。例えば (1/√2)(|0⟩ – |1⟩) という状態では、|1⟩の係数は -1/√2 ですが、観測確率は同じく50%です((-1/√2)² = 1/2)。
・コラム2:量子もつれとノーベル物理学賞
2つの量子ビットが量子もつれ状態にあるとき、片方を測定すると、もう片方の状態が瞬時に決まります。たとえ両者が宇宙の端と端にあってもです。この「不気味な遠隔作用」を嫌ったアインシュタインと、それを実験で証明した科学者たちの壮大な物語が、2022年のノーベル物理学賞の背景にあります。
まず、2量子ビット系の表記について説明しましょう。|00⟩という記号は、「1つ目の量子ビットが0、2つ目の量子ビットも0」という状態を表します。同様に|01⟩は「1つ目が0、2つ目が1」、|10⟩は「1つ目が1、2つ目が0」、|11⟩は「1つ目が1、2つ目が1」です。
典型的な量子もつれ状態:
(1/√2)(|00⟩ + |11⟩)
この状態では、測定すると50%の確率で両方とも0、50%の確率で両方とも1になります。しかし測定前は、どちらになるかは決まっていません。
EPRパラドクス
1935年、アインシュタインはポドルスキー、ローゼンと共に「物理的実在についての量子力学の記述は完全だと考えられるか?」という論文を発表しました。彼らの主張は明快でした:
「物理的性質は測定する前から決まっているはずだ。量子もつれなど、単に私たちが知らない『隠れた変数』があるだけではないか。」
つまり、量子が生成された瞬間に既に「この量子は白、あの量子は黒」と決まっており、観測によって「瞬時に影響が伝わる」わけではない、というのです。
ベルの不等式の発見
1964年、ベルは驚くべき発見をしました。もし隠れた変数が存在するなら、実験結果は「ベルの不等式」という数学的制約を満たすはずだと証明したのです。逆に、この不等式が破れれば、量子もつれは本物だということになります。
2022年のノーベル物理学賞のテーマは「もつれ」?
ジョン・クラウザー(1972年):初めてベルの不等式の破れを実験で確認。量子もつれの存在を世界で初めて実証しました。
アラン・アスペ(1982年):クラウザーの実験の「抜け穴」を塞ぎ、より厳密な条件で量子もつれを証明。光子の偏光フィルターを測定中にランダムに変更することで、測定手法の影響を排除しました。
アントン・ツァイリンガー(近年):最終的な「抜け穴」も塞ぎました。なんと遠い銀河からの信号を使って測定器を制御し、あらゆる古典的説明を不可能にしたのです。
・コラム3:ブラケット表記
量子ビットを|0⟩や|1⟩と書くのを見て、「なぜこんな変わった記号を使うの?」と思ったことはありませんか?この縦線と山括弧の組み合わせは、実は物理学史上最も美しく実用的な記号の一つなのです。このブラケット表記(Dirac記法)の誕生には、量子力学の黎明期を彩る天才たちの知的格闘が隠されています。
ハイゼンベルグの行列力学
1925年、24歳のハイゼンベルクは革命的なアイデアを発表しました。原子内の電子の軌道を「行列」で表現するという、当時としては極めて抽象的な理論でした。
ハイゼンベルクの着想:
物理量(位置、運動量など)を数の表ではなく、無限次元の行列として扱う
例:位置 x → 行列 X、運動量 p → 行列 P
そして XP – PX = iℏ (交換関係)
これは物理学者たちを困惑させました。なぜなら、従来の物理学では「位置×運動量」と「運動量×位置」は同じ値になるはずだったからです。しかしハイゼンベルクは、量子の世界では測定の順序が結果を変えることを数学的に表現したのです。
もっと言えば、今までの物理学は微積分で書かれており、線形代数は馴染みがあまりなかったという話も聞いたことがあります。
ディラックの天才的統合
1930年、ポール・ディラックは行列力学と波動力学を統一する美しい記法を考案しました。それがブラケット表記です。
ディラックの発明:
- ⟨ψ|:「ブラ」(bra)
- |φ⟩:「ケット」(ket)
- ⟨ψ|φ⟩:「ブラケット」(bracket)
この記法の天才的な点は、抽象的な量子状態を具体的な数学操作と直結させたことです。|0⟩は「量子ビットが0の状態」という抽象概念を表しながら、同時に具体的な計算にも使える数学的対象なのです。
ディラックは内積(二つのベクトルの「重なり具合」)を ⟨ψ|φ⟩ と表現しました。これは英語の “bracket”(括弧)に似ているため、彼は左半分を “bra”、右半分を “ket” と名付けたのです。
“bra” + “ket” = “bracket”
おしゃれですね。
現代への影響
ディラックの記法は、今や量子コンピューターや量子情報科学の標準言語となっています。IBMの量子コンピューター「Qiskit」でも、Googleの「Cirq」でも、この記法が使われています。
ハイゼンベルクの抽象的な行列力学から始まり、ディラックの美しい記法によって完成された数学的枠組み。それは単なる記号以上の意味を持ち、量子の不思議な世界を人間が理解するための「言語」そのものなのです。|0⟩と|1⟩という素朴な記号の背後には、20世紀物理学の最も深遠な洞察が込められているのです。
後編

【information】
日本量子コンピューティング協会(JQCA)は「量子エンジニア認定講座」を開催しています。是非皆さんもご参加ください。
https://jqca.org (JQCA公式HP)
検定試験の情報については下記URLを参考にお願いします。









































